Solving the rubik's cube with a genetic algorithm
Algo génétique...
![]()
Note aux francophones : ces quelques pages décrivent l'état d'avancement de mon projet de résolution du cube par un algorithme basé sur la programmation génétique. Désolé, j'ai bien trop de choses à faire pour tout traduire en français, c'est pourquoi seule une version en anglais est disponible. Merci de votre compréhension.
![]()
![]()
The aim of these pages is to describe the state of my project of designing a genetic rubik's cube solving program. Most of the subjects given here have been discussed on Yahoo fewest moves challenge forum, but I thought it would be a good thing to summarize every comments, discussions and ideas here. I'll soon write a better description of the algorithms I am using, but the solver works quite fine now and it's the most important.
May 7th, 2005 : Fewest moves Rubik?s cube solve using genetic algorithm ! (Forum message, Cyril Castella)
Comments and reactions (Messages from Yahoo forum)![]()
May 9th, 2005 : Some words about the beast (Forum message, Cyril Castella)
Comments and reactions (Messages from Yahoo forum)
![]()
May 15th, 2005 : Here is the version 1.0 of the genetic solver ! At the moment, only 2x2x3 building is available, the rest will soon follow
.![]()
May 22nd, 2005 : I was finally able to write the "whole cube genetic solver 2.0" :-) Should solve any given or random scramble, most of the time between 30 and 40 moves for a completely scrambled cube. Chek it out !
July, 5th, 2005 : Version 2.1 : Added one more feature to backup the scramble and the solution in a file. Well ... at least I needed it :)
Some recents FMC scrambles solved by the program are shown here : #81 (33 moves solution), #82 (35 moves solution), #83 (30 moves solution) and the last 2-gen challenge (23 moves solution)![]()
Description of the project
In my academic work, which is related to medical physics, I have met a tough optimization problem and I am trying to solve it using genetic programming. To be short, genetic programming consists in defining a population of n individuals, then evaluate each individual with a fitness function, and use Darwin's rules of selection, mutation and reproduction to evolve to better individuals at each ?generation? and hopefully maximize the fitness function.
How could this be related to FMC ? Actually the progs I developed for my work could easily be translated to this problem, and I chose to adapt Charlie's and Sebastian's approach to solve the cube :
[1] Try to solve the 2x2x3 in Back-Down in fewest moves as possible
[2] Try (1) for the 12 possible 2x2x3 rotations
[3] Get into 2-gen group, using edges orientation check and corners position check (see Sebastian's page)
[4] Solve the cube in the (F,U) group
The question was ? was it going to work ? I have no definitive answer, as no ?serious? validation was made and there are still lots of parameters I can tune in the genetic alg, but I fed it with #82 FMC scramble and here is I got a really cool 35 moves solution (see details here) not bad for a first try in FMC challenge ;-)
So now ? why am I telling you all this ? I thought it would be great to use your experience to improve the performance of the algorithms. The question I am trying to answer is : ?what is the best mean to compute short, human-understandable solutions ??
One of the best approaches to find a short solution (probably the best one ?) is Kociemba's alg, but as we all noticed there is no way one could figure out such a solution ?
Lars' general method is good but there is a need to know quite a lot o LL algs to be really efficient in terms of metrics
Fridrich is definitely not a good FM method ?I don't think any further discussion about this method is needed :)
Gilles' methods seems very interesting, but I doubt I could implement it easily in my program. The drawback of his approach is the STM optimization ? but quite bad in HTM. Actually a ?standard? solution (with ?normal? opposite 1x2x3 blocks) should not be too hard to program ?
?solving all but some edges/corners? should be possible to implement, I will think about that. The point is to define an efficient fitness function for that task. And the alg insertion promise tough problems to solve...
pseudo-moves are quite easy to figure out for a human solver, but apart from trying all 18 possible moves before the scramble (or 18*15 or 18*15*15 or ?) I don't see any efficient way to implement it in a genetic alg.
What about other ideas ?
I think I will describe this project more precisely in a few weeks (fitness functions used, performance, ?), when the beta version is more ready, and of course let you test the code on random scrambles if you're interested ! The aim of this post is to have some feedback about other FMC techniques I could have missed, I strongly encourage you to reply :) At the beginning (and even now, but with a little less hope ?) I thought genetic algs could offer an elegant alternative to kociemba's ?brute force? optimal solutions, without any table or known alg, but the whole cube solve seems to be a really tough problem for GA. Let the future answer this question !
Comments after the first post
from : Per Kristen Fredlund :
Hi Cyril!
Interesting post. I know a little about gentic algorithms. Could u describe more how ur approach works. How do u evaluate good and bad "species"? More specifically how do u define fitness functions? And how do u perform crossover and mutation? Do u at all have some built-in "cube-knowledge" in ur code?
U also mention some approaches solving cube effciently and "human-like". Can't see that u have listed the popular approach to FMC, namely blockstyle. For blockstyle beginning u have many alternative
paths to take. After say 2x2x2 and 2x2x3 u can either:
- do f2l, then rest by OLL + PLL (or replace OLL and PLL with an alg that leaves either corner or edge 3-cycle to be inserted ... here my planned but not realised alg-insertion program could be handy)
- orient edges and fix corners so that u end up with 2-G finish ... u have already looked at 2-G using GA so this is maybe a very interesting path for u
- do all edges and finish off with a bunch of corner cycle insertions
- do all corners and finish with some edge-cycle insertions
- do ZBf2l for easier LL
- do f2l minus 1 c/e pair, orient all corners, then rest
Just to mention a few of the most common ones :-)
Cheers!
-Per![]()
from : Michiel van der Blonk :
Hi
Fantastic. I have also been working on a genetic solver for a while now, in a deep secret underground factory, preparing for world domination. And I have come up with a different technique. I am connecting pairs of cubies and just optimize that. This is just a first step, and it appears to be a pretty devious problem to tackle.
I hoped to just magically see a solved cube, but... not yet. My program is written in VBA. I will convert it to VB and then later maybe VB.NET (or even C or Java) for speed.
A solved cube has 72 connected pairs. The program jumps pretty quick from a start of 9 pairs to say 20-30 pairs. That's when it starts to slow down. 40-50 pairs is usually a solution with only 3 or 4 cubies incorrectly placed or oriented.
My first solver was a python program, but that one was for the 2x2 and didn't use the right search path , so it led to nothing.
I am willing to share my code and work with others on a better solver, so when I have mine prepared I will post it to the group. If you like a copy, please email me. It's a self-explaining Excel file with a cube view and a scramble and solve button.
I really think this kind of program could have a huge potential in looking for a good solution, and maybe even more human-readable than the brute force programs.
bye
Michiel![]()
from : Lars Petrus :
I spent a weekend a few months back working on something similar. I came up with 3-4 more or less advanced metrics and tried to weigh them. It got pretty far, but never actually solved the cube.
I'll never finish it, so I'd be happy to work with others as well.
/Lars![]()
from : Charles Tsai :
Oh jeez, all coming out of the woodwork now :)
Cyril, a while ago I was thinking of writing a solver by ending with 2-gen to see what the limits of this method were but I could never get myself motivated to think and figure it out.. So, good to see you do it! Using this method in the fmc, i think it's probably around 30, maybe slightly less but not much.. Do one of the 12 2x2x3s, then instead of immediately getting into 2-gen (which is what I do) do some R,U turns and then flip the edges and fix the corners and then finish with more R,U turns.
Maybe a program that would use different methods depending on some property of the scramble? You know, if the scramble had a certain property, use method X, if another property, use method Y. Maybe I should be doing the same thing in FMC, instead of 2x2x2 then 2x2x3 etc the same way every time. I have no idea what these properties
would be however... ;)
Since we're on the topic of cube programs: I too worked on a cube program in my own ultra-secret underground cave!!! Back when Per was talking about his alg-inserter, I mentioned that I wanted to write a solver for the 4x4x4. Well, it only partially solves it: only edges and corners, but not centers. In under 50 moves usually. I've pretty
much abandoned it, I haven't done anything with it for several months now
Charles![]()
from : Gilles Roux :
Building blocks looks nice at first, but you quickly realize that a nice looking pre-PLL cube is still more than 10 moves away from the solution (travelling through positions with much fewer blocks)...
Optimization functions are really hard to find. No surprise, that's why it's so difficult to solve a cube in 20 moves!!
Cyril, tell us more about your algorithms :-)
Gilles.![]()
Some words about the beast
Lots of comments, many thanks to all of you ! It seems that many of us have such a secret dream to become a new Kociemba :) I had a lot of fun when I noticed that within a few hours your comments were really coming from all parts of the world (France, USA, No-way, Santa Cruz, ?)
I don't have much time and as told you these are only preliminary results, but here are the facts. The names after the titles are related to some of your recent posts and questions on that topic.
1) Blocks, facelets, pairs ? (Michiel, Gilles)
2) The solving method I implemented (Per, Charles)
3) Fitness functions (Lars, Gilles, Per)
4) Other GA parameters (GA = genetic alg) (Per, Gilles)
1) I first tried the most obvious way : defining a cube as 54 facelets, optimizing the number of facelets matching a solved cube. He he he would say Per ! It is actually possible to converge to about 40 corrects ?stickers?, but then impossible to solve the cube quickly, since all incorrect pieces are disseminated on all faces. So I decided to define kind of a "cube entropy", using that definition : entropy = -(sum[CEp] + sum[ECep]) , where a CEp is a corner-edge pair (WHICH IS REALLY CORRECT, as opposite to Michiel's more permissive definition, see his post), and ECep is an Edge-center pair. Entropy of a solve cube is 48, entropy of a random cube is ? I actually never looked at, but probably around 3 to 6 (?) So in terms of pairs a 2x2x3 is built with 16 ?pairs?.
2) Actually I used a block method. I wrote I implemented Charle's and Sebastian's way, perhaps I should have been more explicit : I look for a "good" 2x2x3, THEN jump into the 2-gen group THEN try to solve the cube in the 2-gen group. I will think about the other methods you mention after the 2x2x3, but I really want to keep my GA "memory-free", without using any LL alg or built-in insertion technique. At the moment is really using only Darwin's laws, and Darwin did not know a single Rubik's cube alg ;-)
3) THIS IS THE POINT !
What do we all want to do when participating to FMC ? Eventually solve the cube ... and minimize the number of moves. My fitness functions are no less than a mathematical expression of this fact : when evaluating a 30-moves individual of the population (say for the 2x2x3 stage) I use that procedure :
Nmax = 0, Jmax = 0
For j = 1, 30
Do move j
N = -entropy of the 2x2x3 location (between 0 and 16)
If N>Nmax then Nmax = N and Jmax = j
End for
Fitness = 10Nmax-Jmax
That is, at a given stage of the optimization process, I will allow longer solutions to be well rated, if they build more pairs than other shorter solutions. The factor 10 is purely empirical :)
For getting into the 2-gen group I decided not to teach the alg any moves sequence. Starting with the 2x2x3 already built, I simply tell my GA that he can break it only for a short time : the procedure is exactly the same, except that N = is2gen + 100is2x2x3, where is2gen is a Boolean variable telling if the edges are correctly oriented AND the corners correctly positioned to be solvable in the 2-gen group (thanks to Sebastian for the elegant way to define it), and is2x2x3 is another Boolean variable to tell if the 2x2x3 is still alive. This fitness function makes sure the alg will not come up with a broken 2x2x3 at the end of the stage, which could be problematic for the edges/corners checks.
Then the 2-gen part is solved using N = -entropy, which still has the bad habit to converge in too many situations to a value of 42 instead of 48: 2 twisted corners :(
4) Just to be short, I use : elitist GA (best individual of a generation is kept) / pop_size = 51 / mutation prob = 0.05 / crossover prob = 0.8 / parents selection by rank (best parents are more likely to have children ? do not try to compare with real life ?) / each individual is a string of 30 integers
A crossover is a gene exchange with crossover point at random location, a mutation is the replacement of a gene by another random one.
I played with the idea of "diseases" in the population, and I kill the 5 weakest individuals at each generation and replace them with random individuals. I'm probably not the first to have that idea ?
OK, that's all folks ! I will make a webpage on my site with all your suggestions and the state of advancement of this solver, and post my FORTRAN codes once they are more presentable (at the present time it is just a bunch of codes lines with tons of unnecessary comments !)
Reactions after the second post
from : Michiel van der Blonk :
--- "Cyril Castella" <cyrilca@c...> shouts:
> to define kind of a "cube entropy", using that definition : entropy = -(sum[CEp] + sum[ECep]) , where a CEp is a corner-edge pair (WHICH IS REALLY CORRECT, as opposite to Michiel's more permissive definition
I don't think either one of us is 'more correct' on the topic. I chose the word pair because that is what it is: a pair of facelets. It's not a pair in the way we form F2L using 'pairs' which are always pairs of an aligned edge and corner. In fact in my program, such a pair can be described just as easily as a collection of 'simple pairs'.
> the moment is really using only Darwin's laws, and Darwin did not know a single Rubik's cube alg ;-)
But I think if he did he'd be a darned good speedcuber.
> Elitist GA
I usually use this one too.
> each individual is a string of 30 integers representing a solution
how?
> A crossover is a gene exchange with crossover point at random location, a mutation is the replacement of a gene by another random one.
How is a gene defined?
> I played with the idea of "diseases" in the population, and I kill the 5 weakest individuals at each generation and replace them with random individuals. I'm probably not the first to have that idea …
It's new to me. I usually use mutation only.
> and post my FORTRAN codes once they are more presentable
FORTRAN! That's a golden oldy. I might still have my GA library in Pascal somewhere. My most fun GA used to be one that wrote a program for getting out of a maze. But the cube is more fascinating.
BTW: how many times does it find a solution, and in how many generations? Does it need a lot of processing power?
I'm looking forward to seeing it.
Michiel
My answer to Michiel's questions :
Hi michiel,
just some more comments :
Of course I did not meant that "my" definition of a pair was more clever than "yours", I just wanted to point out that in my case a Corner-Edge pair is a "F2L corner-edge pair". I really think it is more efficient for converging to the solved 2x2x3 or whole cube.
A gene is an integer representing a move : 0-5 = FURBDL, 6-11 = F2... L2, 12-17 = F'...L'. An individual is therefore a sequence of 30 moves. But the fitness function is not necessarly defined for the whole sequence, but at the best point (see the definition of Jmax in the pseudo-code I gave in my last post). That really makes a difference, IMH... I use a "trim function" to remove cancelling moves and add random moves at the end of a trimmed individual after crossover or mutation processes.
To obtain the whole solution, I used about 3 hours computing time. About 12 x 10'000 generations (12 x 3 minutes) for finding a good 2x2x3, then about a minute to find a good way to get into 2-gen group, then ~2 hours to solve the 2-gen group. I only tested a few scrambles, but it seems to be reliable (it found a nice 23 moves solution for #58 2-gen FMC)
Cheers !
Cyril![]()
from : Sebastian Dumitrescu :
Cyril Castella wrote :
> telling if the edges are correctly oriented AND the corners correctly positioned to be solvable in the 2-gen group (thanks to Sebastian for the elegant way to define it)
Hi Cyril and others!
I'm very glad that I could contribute with something for this, but I still don't understand the main idea of genetic algorithms. I won't try to understand the FORTRAN code or any other code, I just want somebody to explain the extra-basic idea of the GA. Can it be mathematically represented as a function or as a composition of functions? How can it be associated with the cube moves?
I know that this has been explained, but I would really like to understand this better.
Thanks,
Sebastian![]()
from : Lars Petrus :
I don't know much about genetic programming, and I probably did that part mediocrily at best, but I have a bit more ambitious fitness function than what I've heard mentioned so far. By fitness function I mean something that measures how close a position is to the solved state.
First consider the "Connectivity Number", which I'll define as the number of formed pairs. There are 24 such corner/edge pairs and 24 center/edge pairs. One move can only change either number by 4 or less. You can use this for "backtracking" problems (when you want to trace back n moves) since you know that when there are x moves left, each Connectivity Number has to be at least 24 - (4 * x).
The advanced part is to take into account that unformed pairs can be more or less close to being formed. A corner/edge pair can be up to 3 moves from being joined, while a center/edge pair is at most 2 moves away. So for each corner/edge pair you have a number from 0 to 3, and for each center/edge pair a number from 0-2. In total that gives a corner number from 0 to 72 and a center number from 0 to 48.
Having watched the program trying to solve using this metric it's not hard to get more ideas on how to refine it.
Lars
Comments on Lars' idea by Gilles Roux :
--- Lars Petrus <lars@l...> wrote:
> The advanced part is to take into account that unformed pairs can be more or less close to being formed. A corner/edge pair can be up to 3 moves from being joined, while a center/edge pair is at most 2 moves away. So for each corner/edge pair you have a number from 0 to 3, and for each center/edge pair a number from 0-2. In total that gives a corner number from 0 to 72 and a center number from 0 to 48.
It's a bit more ambitious, but does it give interesting results? On very easy cases, almost solved, an objective function based on these criteria looks nice, more powerful. But I think it's still inefficient, because the problem comes from other global constraints. You can make a pair in 2 moves and another one in 3 moves, but 7 moves are required if you want both.
When I was young, I was dreaming of such fitness functions. The more I cube, the more I realize how naïve I was. Now I'm very skeptical :-)
Gilles![]()
from : Stefan Pochmann :
I think the major problem is not the number of states, but that it's hard to find a valid solution at all and mutate it to another solution.
A traveling salesman instance with let's say 100 cities has far more states but all of them are solutions (well, unless of course you add restrictions), they just differ in their length. Mutation can be done by simple things like swapping two cities.
Have you seen Tom's cube contest? The three top solutions used Thistlethwaite, fourth place used large searches, but fifth place (David Barr's solution) uses a human-like solution and averaged 35.03 moves (though only half of the scrambles were really random, the others were scrambled with up to three moves only, but then again if the program uses a fixed order it might still take many moves even for such a scramble... don't know, haven't checked).
http://tomas.rokicki.com/cubecontest/winners
Cheers!
Stefan Pochmann
![]()
Version 1.0
Okay ... Here is version 1.0 of the genetic solver. Main charactersitics are listed below :
- I only automatised the 2x2x3 search over the 12 possible locations
- Scramble types : random or used-defined
- Scramble length : user-defined
- Fitness function : 10 x Np-Nm, where Np is the number of correct pairs (either Center-Edge or Corner-Edge) at the 2x2x3 location and Nm the number of moves. Programs indicates the value of the fitness function, the number of moves, and Np, at the end of each location simulation. Np = 16 means the 2x2x3 is solved.
- The solver turns the cube (actually in a weird way for some locations ...) after scramble to place the 2x2x3 to solve in BD. Do not forget to add the indicated cube rotations (y's and/or xy's) at the beginning of the given solution !
- Notation for scramble : please use only FRUBDL, F'R' ... L', F2R2 ... L2.
- For a real random scramble (say at least 25 moves), the solver may find some solutions with 10'000 generations/location, and should find sub-20 moves for nearly each location with 50'000 generations. Remember however that it's only a "1.0" version !
Features to come with next versions include of course completely automatised cube solving, nicer user-defined scramble possibilities, error messages when error occurs and a lot of more things I have to fix ;-) Please don't blame me for all infinite loops you'll meet when making errors while entering the scrambles !
Version 2.1
Latest version :
Download Windows executable (429 ko) : genetic21.exe . Should run nicely under all windows versions...
Download source code (fortran 90, open it with any text editor).
Rubik's cube genetic solver, version 2.1
Added the automatic backup of the scramble and the solution in a txt file.
Rubik's cube genetic solver, version 2.0
What's new since 1.0 ?
Solver now solves the whole cube automatically
User-defined (manual entry of each move, sorry !) or random scramble
Automatically increments the number of generations if no good solution is found for a given stage of the process. Defaults are 50'000 for the 2x2x3 search (or less, since it's user-defined), 10'000 for getting into 2-gen part and 200'000 for solving the 2-gen. This should lead to 30 to 40 moves solutions for well scrambled cubes. Computing time obviously stringly depends on the number of generations for 2x2x3 stage, but sould be around 3 hours for these settings.
Fixed some bugs for 2-gen corners positions check and for the cube rotation to visit all 12 locations. Fixed another bug which conducted to some really nice infinite loops ...
Screenshot: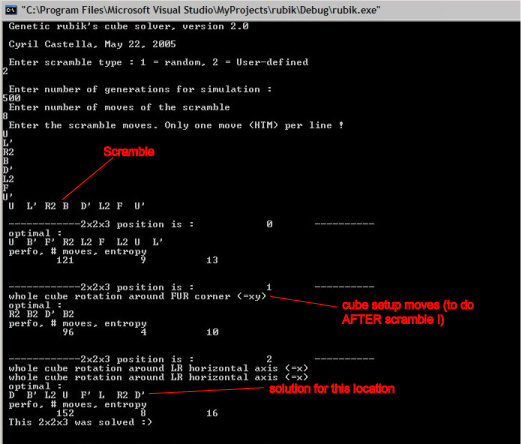
Scramble :
F2 (U R' L' F)*4 B2 U' R' D2 (F R B2 U2)*4 D (FMC #81)
Solution steps :
[1] Try to solve the 2x2x3 in Back-Down in fewest moves as possible
[2] Try (1) for the 12 possible 2x2x3 rotations
For these two stages, 50'000 generations/location led to 4 sub-13 moves solutions (2x9, 11, 12, 2x13, 3x15, 16, 17, 23), I picked one of the 9's : yRL2B'L'D'R'BL'B'. Note that for each location a solution was found.
[3] Get into 2-gen group, using edges orientation check and corners position check (see Sebastian's page)
5000 generations were enough to find the 5-moves solution : RUR2F2R
[4] Solve the cube in the (F,U) group
That was the long part : 427'000 generations to find the elegant 19-moves FU'F'U'F'U2F'U2F2U'F'U'F'U'FUF'UF'.
TOTAL : 9 + 5 + 19 = 33 moves
Scramble :
D2 R' B2 D2 (L' F2 B' D2 F' )*3 U' B U2 B' F' (R F' B U D2 )*3 F U B' F' (FMC #82)
Solution steps :
[1] Try to solve the 2x2x3 in Back-Down in fewest moves as possible
[2] Try (1) for the 12 possible 2x2x3 rotations
I made a search of about 1 minute (computing time) for 8 locations and the shortest solution found was xyL'B'L'URB'U2R2BR2F2L2 (12 moves HTM). I'm quite certain it is possible to do better with longer search time ? The genetic alg found 13-14-15 or 16 moves solutions for other locations
[3] Get into 2-gen group, using edges orientation check and corners position check (see Sebastian's page)
I decided not to use any table or known alg for this part, and let the alg find a 6-moves sequence to get into the 2-gen group : U2LF'L2U'L
[4] Solve the cube in the (F,U) group
The alg found in about 1 hour a 21 moves sequence to solve the 2-gen group, and reduced it to 17 after another hour search : F2U'F2U'F2U'FU'F2U'F'U'F2U'F2U'F
TOTAL : 12 + 6 + 17 = 35 moves
Scramble :
R D R B L2 (D B' L F)*3 R2 D F' (U2 B R D')*3 L2 R D U2 F2 (FMC #82)
Solution steps :
[1] Try to solve the 2x2x3 in Back-Down in fewest moves as possible
[2] Try (1) for the 12 possible 2x2x3 rotations
With the version 2.0 of the solver, I searched during 50'000 generations for each of the 12 locations. Best solution was given by xyD'L'BRL'BU'F2BL2 : 10 moves for a good start !
[3] Get into 2-gen group, using edges orientation check and corners position check (see Sebastian's page)
Since 4 bad edges need to be fixed, the solution is here not especially short : FRU'R2F'R
[4] Solve the cube in the (F,U) group
It took only 10'000 generations in this phase to solve the 2-gen group in 14 moves, for an excellent final result of 30 : UF'U'F2U2FUFU'F2U2FU'F
TOTAL : 10 + 6 + 14 = 30 moves
Scramble :
(FUF2U')*3F2U2F'(UF2U'F)*3U2F'UF2(U'F'U2F)*3 (FMC #82)
Solution steps :
[4]Solve the cube in the (F,U) group
That was really fast (13'000 generations, ~2 minutes computing time) : F2U2F'UF'U'FU2FUF'U2FUF2U2F2U'F2U'F2U'F'

